Вот и закончилось лето!
Жаль!
Ведь вместе с летом закончились веселые школьные каникулы.
Детвора снова пойдет в школу.
И все повторится как в первый раз – и первый звонок, и рассказы сверстников, и официоз классов.
Как мираж рассеется воображаемая свобода.
И начнутся серые школьные будни с различными домашними заданиями и нудными учителями, которые не давали нам покой даже летом, отравляя нашу жизнь своими теориями и практиками, внося сумятицу в стройные ряды различных сообществ, навешивая «ярлыки» и раздавая «оценки».
И то, что не было понято нами в прошлом году, учителя требуют отработать в году будущем.
Только поэтому вместо того, чтобы готовить сочинение об отношениях мальчиков и девочек под названием «Как я провел лето», мне приходиться писать о геометрии.
Я получил «неуд» по «подобию треугольников».
И наш учитель, кстати, член вашего сообщества, предложил мне сдать эту тему письменно и вынести ее на всеобщее обсуждение.
Итак, «подобие треугольников»! (далее «Т.»)
1)Подобие «несовершенных» Т. – т.е. «разносторонних» доказать легко.
Есть 3 признака подобия, и я не стал списывать их из др. источников.
2) Проблема состоит в том, чтобы доказать подобие «правильных» Т.
3) Когда Т. стремятся стать «правильными» ( с равными свойствами, углами, сторонами), то они становятся очень похожими др. на друга.
Отсюда следует определение:
4) «Правильные» Т., большие и маленькие, устремленные вверх и вниз, все как один подобны.
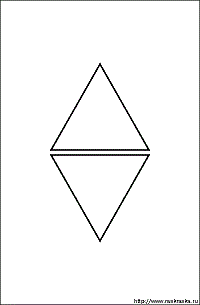
5) Остается выяснить, какое подобие лучше, какое важней? (см. Рисунки)
И тут, согласно рисункам, возможны два варианта похожести, если за основу берется «высший» Т.
Рис.1
Рис.2
Первый вариант: Быть каким угодно маленьким, но включенным в «высший» Т.
А если даже и ощущать себя внизу, но стремиться вверх.
Второй вариант: Быть не просто подобным «высшему» Т., но и иметь с ним одно жизненное основание, быть равным ему,… но перевернутым в зеркальном отражении по типу «печать и отпечаток».
Какие же Т. более подобны между собой? Маленький внутри «высшего» или равный, но «обратный»?
Я за первый вариант, а учитель за второй.
Я объяснял, видя раздражение учителя, что здесь нет конфликта.
Что подобно теории относительности Эйнштейна, где есть Общая и Специальная теории, в данном случае мы имеем дело с геометрией Лобачевского, как Общей теорией и геометрией Евклида, как частным случаем первой. Так вот второй вариант подобия, конечно же, весомее первого с точки зрения геометрии на примитивной плоскости, где равенство апогей подобия. А вот с точки зрения геометрии Лобачевского, геометрии высшего пространства, Т. на Рис.1 не только подобны, но также равны, и не просто равны, а находятся в одном месте, накладываются др. на друга.
Налицо три преимущества подобия против двух.
Что тут началось!
Учитель кричал о том, что в нашей материальной жизни не нужна геометрия высшего пространства, что он мечтал научить нас прикладной геометрии.
Что счастье в этом мире заключается в том, чтобы понимать «свои» Т. и анализировать «чужие».
Что наше естество ниже любого Т.
Что добиться успеха в жизни можно только разобрав первобытную геометрию на уровне инстинктов.
Что наука о «высшем» и «низшем» мире – это по сути одно и то же, как наука о душе и прикладная психология.
Я ответил, что знать основы материального, низшего мира, конечно же, стоит.
Но, для чего? Чтобы раскладывать его на треугольники счастья?
Аналитические способности и ощущения счастья не накапливаются в Высшем.
Знать о себе и о мире «Все» – это не значит знать Мир.
Высший и низший треугольники на втором рисунке, точно также как и высший и низший миры, конечно же, равны и даже опираются на одно жизненное основание… Только вот что делать с их противоположностью.
И еще. Великие геометры умерли. Уйдут и великие учителя. И народ забудет их могилы.
Через сотни лет люди помнят, чтут и ищут только могилы тех, кому ничего не нужно было от этого мира, подобно маленькому Т. внутри Большого – добавил я.
Добавил и получил «неуд».
Жаль!
Ведь вместе с летом закончились веселые школьные каникулы.
Детвора снова пойдет в школу.
И все повторится как в первый раз – и первый звонок, и рассказы сверстников, и официоз классов.
Как мираж рассеется воображаемая свобода.
И начнутся серые школьные будни с различными домашними заданиями и нудными учителями, которые не давали нам покой даже летом, отравляя нашу жизнь своими теориями и практиками, внося сумятицу в стройные ряды различных сообществ, навешивая «ярлыки» и раздавая «оценки».
И то, что не было понято нами в прошлом году, учителя требуют отработать в году будущем.
Только поэтому вместо того, чтобы готовить сочинение об отношениях мальчиков и девочек под названием «Как я провел лето», мне приходиться писать о геометрии.
Я получил «неуд» по «подобию треугольников».
И наш учитель, кстати, член вашего сообщества, предложил мне сдать эту тему письменно и вынести ее на всеобщее обсуждение.
Итак, «подобие треугольников»! (далее «Т.»)
1)Подобие «несовершенных» Т. – т.е. «разносторонних» доказать легко.
Есть 3 признака подобия, и я не стал списывать их из др. источников.
2) Проблема состоит в том, чтобы доказать подобие «правильных» Т.
3) Когда Т. стремятся стать «правильными» ( с равными свойствами, углами, сторонами), то они становятся очень похожими др. на друга.
Отсюда следует определение:
4) «Правильные» Т., большие и маленькие, устремленные вверх и вниз, все как один подобны.
5) Остается выяснить, какое подобие лучше, какое важней? (см. Рисунки)
И тут, согласно рисункам, возможны два варианта похожести, если за основу берется «высший» Т.
Рис.1
Рис.2
Первый вариант: Быть каким угодно маленьким, но включенным в «высший» Т.
А если даже и ощущать себя внизу, но стремиться вверх.
Второй вариант: Быть не просто подобным «высшему» Т., но и иметь с ним одно жизненное основание, быть равным ему,… но перевернутым в зеркальном отражении по типу «печать и отпечаток».
Какие же Т. более подобны между собой? Маленький внутри «высшего» или равный, но «обратный»?
Я за первый вариант, а учитель за второй.
Я объяснял, видя раздражение учителя, что здесь нет конфликта.
Что подобно теории относительности Эйнштейна, где есть Общая и Специальная теории, в данном случае мы имеем дело с геометрией Лобачевского, как Общей теорией и геометрией Евклида, как частным случаем первой. Так вот второй вариант подобия, конечно же, весомее первого с точки зрения геометрии на примитивной плоскости, где равенство апогей подобия. А вот с точки зрения геометрии Лобачевского, геометрии высшего пространства, Т. на Рис.1 не только подобны, но также равны, и не просто равны, а находятся в одном месте, накладываются др. на друга.
Налицо три преимущества подобия против двух.
Что тут началось!
Учитель кричал о том, что в нашей материальной жизни не нужна геометрия высшего пространства, что он мечтал научить нас прикладной геометрии.
Что счастье в этом мире заключается в том, чтобы понимать «свои» Т. и анализировать «чужие».
Что наше естество ниже любого Т.
Что добиться успеха в жизни можно только разобрав первобытную геометрию на уровне инстинктов.
Что наука о «высшем» и «низшем» мире – это по сути одно и то же, как наука о душе и прикладная психология.
Я ответил, что знать основы материального, низшего мира, конечно же, стоит.
Но, для чего? Чтобы раскладывать его на треугольники счастья?
Аналитические способности и ощущения счастья не накапливаются в Высшем.
Знать о себе и о мире «Все» – это не значит знать Мир.
Высший и низший треугольники на втором рисунке, точно также как и высший и низший миры, конечно же, равны и даже опираются на одно жизненное основание… Только вот что делать с их противоположностью.
И еще. Великие геометры умерли. Уйдут и великие учителя. И народ забудет их могилы.
Через сотни лет люди помнят, чтут и ищут только могилы тех, кому ничего не нужно было от этого мира, подобно маленькому Т. внутри Большого – добавил я.
Добавил и получил «неуд».

Комментариев нет:
Отправить комментарий